March 6, 2023

The most rational man I ever met, whom I shall call Ysidro, … [w]hen told that he did not satisfy all of the v. Newmann-Morgenstern axioms, he replied that he thought it more rational to satisfy his preferences and let the axioms satisfy themselves.

Suppose we have a 100-sided die, and we’re looking at the following gambles whose outcomes are determined by a single roll of the die:

When presented with a choice between 1A and 1B, then between 2A and 2B, it’s common for people to choose 1A and 2B. This is the Allais paradox, so named because it goes against a seemingly obvious principle: When choosing between two gambles, a change in an outcome they share shouldn’t change our preference. In this example, changing what happens when the die lands on 1 through 89 can change whether people prefer the A gamble or the B one.

This phenomenon is interesting to decision theorists and behavioral economists, who seek to answer the following questions:

• Is the Allais paradox an example of rational decision making?
• If so, how is it justified?
• If not, why do people make the wrong choice?

But hang on a minute—how common is the Allais paradox anyway? Are we even sure this is a real thing?

It’s probably a real thing

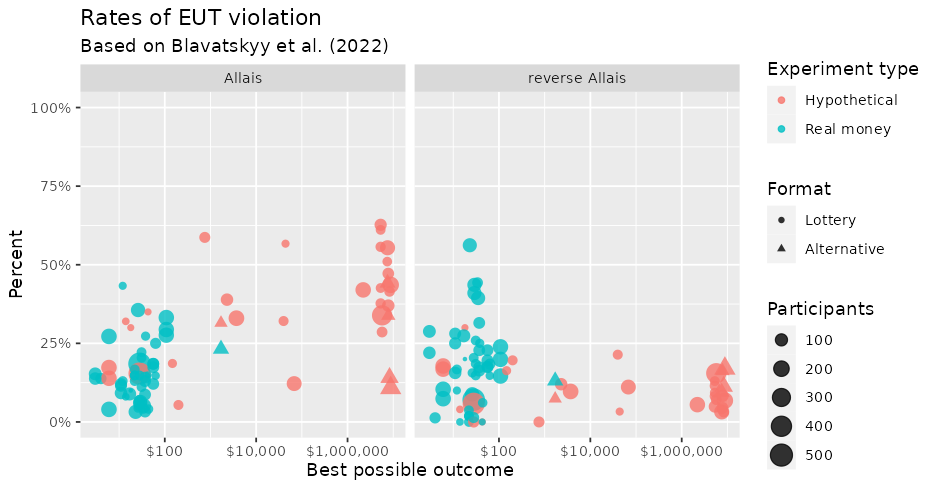
In the article “On the Experimental Robustness of the Allais Paradox”, the authors compiled the results of 81 surveys that tested the Allais paradox. Of course, the paradox in its original form would be prohibitively expensive to test, so the surveys were a mix of hypothetical lotteries, where nobody actually won anything, and real lotteries with dramatically lower stakes.

The authors found that while many people did choose 1A and 2B, just like in the Allais paradox, it was also not unusual for people to choose 1B and 2A, a reverse Allais choice. Personally I find this totally baffling, but whatever. Either of these would be a violation of expected utility theory (EUT), and for similar reasons.

It’s clear from the picture that you’re more likely to see the Allais paradox if the potential winnings are huge, and this can’t just be blamed on the lack of real stakes. The two triangles in the bottom-right corner of the Allais plot involved surveys that were specially designed to avoid the Allais paradox, so I’m not too bothered by them. I’m also not bothered by the lack of real money experiments with millions of dollars at stake, just because I don’t see why someone would lie about their preferences here. On the other hand, there’s a lack of variety in the surveys with huge hypothetical winnings. (The plot doesn’t reflect this, but you can see it if you read the original paper.) So while the Allais paradox is probably a real thing that happens when the stakes are high, there’s still a lot that we just don’t know about it.

“Money pumps” that aren’t

Believing the Allais paradox is irrational, some people have tried to come up with ways of exploiting it. Here’s an example of how this might work:

1. Suppose we flip a coin. If it lands heads, then you get gamble 1B. If it lands tails, you get gamble 2A.
2. Now suppose that after flipping the coin, I offer you a choice. If the coin lands heads, you can switch to a slightly worse version of gamble 1A. You still prefer it to 1B, but it’s not as good—say you win $999,999 instead of the full $1 million. Likewise, if the coin lands tails, I offer the switch to a worsened gamble 2B.
3. From a certain point of view, you are determined to make trades that leave you worse off no matter what happens.

This is basically what is going on in the recently published article “Money-Pump Arguments.” Big Yud made a similar argument when he wrote about the Allais paradox. The most striking thing about these so-called money pumps is that they do not pump money. They do not guarantee a profit for the person running them, not even in the long run. This isn’t like with nontransitive preferences, where you can trade with someone in a cycle forever. To the people who think the Allais paradox is clearly irrational, I ask: Why can’t you make a real money pump?

My perspective

I think the lesson here is simple. Newtonian mechanics doesn’t work when there are huge speeds involved, and expected utility theory doesn’t work when there are huge sums of money involved. These are both useful approximations of a larger, more complete theory that we don’t fully understand yet. The world is a complicated place. People who embody the Allais paradox are probably using a heuristic that makes sense in exceptional circumstances. I think it’s foolish to dismiss it as just another example of irrationality.