February 11, 2023

A recently published study has been making the rounds on rationalist blogs. Scott mentioned it in his links post (#46), then Zvi picked it up. Both were completely credulous. The headline, in Zvi’s words: “Flashing lights at the proper intervals increases learning by a factor of three.” Because brain waves.

Before talking about the paper itself, I want to point out that this effect size is implausible, so we can immediately dismiss it. I’m going to elaborate on that, but I wanted to say this up front. Because seriously, everyone is being way too credulous here. For example, here’s Zvi:

If you take this hypothesis seriously, even giving it a 1% chance it would work, you wouldn’t risk waiting around to see what happens. You wouldn’t wait for formal Proper Science to slowly study it. You’d test it, in the real world.

The claimed effect is a priori implausible, and the evidence is miniscule. If we want to give this claim a probability, it should be a lot closer to 0% than 1%.

The study design

The researchers recruited 80 healthy young adults and divided them into four groups of 20. The experiment took place over two days. On the first day, everyone was shown a sequence of noisy dot patterns on a computer screen. Participants were asked to classify each pattern as “radial” or “concentric.” Before each pattern, the participants were shown a light that flickered for 1.5 seconds. There were three kinds of flicker:

• a regular frequency that matched participants’ alpha waves
• a regular frequency that didn’t match the alpha waves
• a randomly changing frequency

Likewise, there were two times when participants could be shown the patterns: “peak” times or “trough” times. And I’m not going to delve into the details here. The point is, there are six possible timing combinations, but the experimenters only had four groups to work with. As I understand it, the groups worked like this:

The second day was similar to the first day except there was no flicker. The thing to notice here is that the experimenters varied both the flicker and the time when they showed the patterns. So even if the effect is real, it’s pretty much useless. Nobody’s going to be integrating light shows into college lectures because of this.

There’s problems

In the paper, the authors claim that they’ve uploaded their data to Apollo, a repository provided by Cambridge University. But this isn’t true. They’ve actually uploaded several files full of summary statistics. The raw data is “available upon request”—also known as “not available.” For what it’s worth, I emailed one of the authors and asked for the raw data. We’ll see if anything comes of that. (And no, I did not mention this snarky article.)

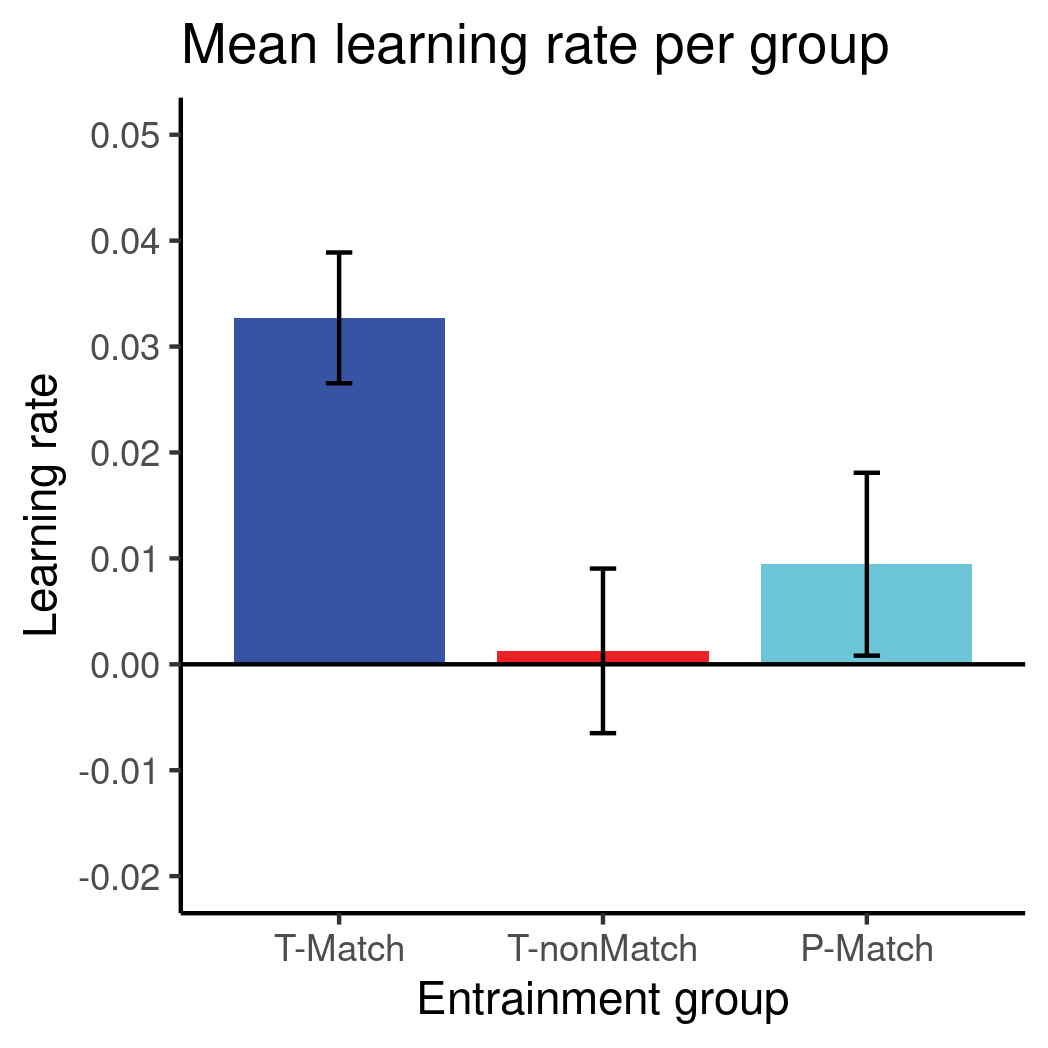
Nevertheless, I was able to replicate one of the figures in the paper using the summary data. (File groupLR_forLMM.csv on Apollo.) It’s the figure featured in this blog post, the one that apparently started all of this. The figure shows three of the four groups (why only three?) and their average “learning rates.”

What’s a learning rate? Basically, the authors tracked each participant’s classification accuracy over time, and fit a logarithmic curve \(y = \alpha + \beta \log x\) to the data. The parameter \(\beta\) is the “learning rate.” A few problems here:

• It’s unclear if these curves fit the data well. The authors didn’t make any pictures, so without the raw data I can’t say.
• About a third of the participants had negative values of \(\beta\). This would seem to suggest they got worse over time. If you wanted to measure people’s ability to learn, shouldn’t you use a task people can reliably learn to do?
• Seeing as how the learning rate can be negative, it isn’t appropriate to say things like “three times faster.” If you had a rate of zero, would you say “infinity times faster”? (To their credit, the authors didn’t use that phrase. But this article published by Cambridge did.)

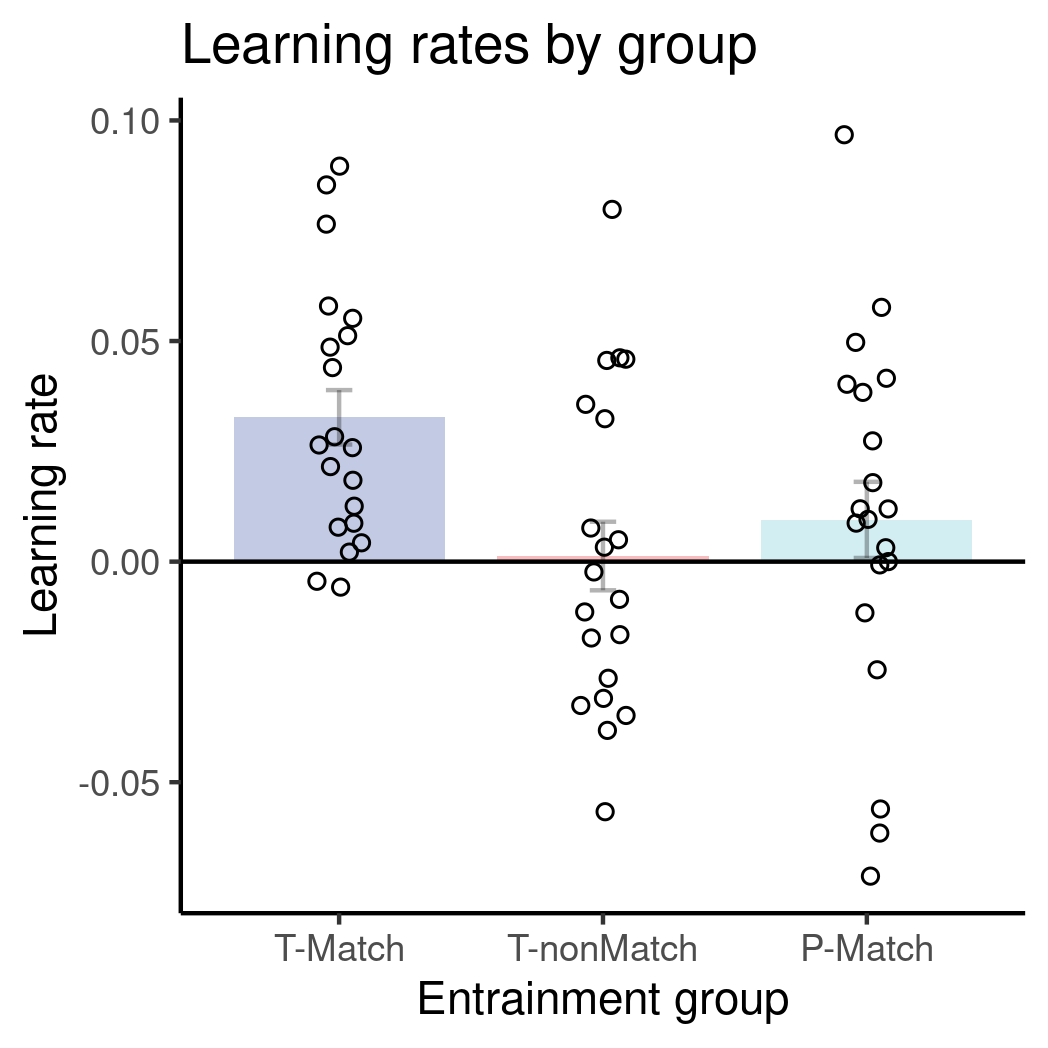
I also made a plot that shows the data for those three bars. It looks a lot less impressive. Sorta makes you think the authors just got lucky.

At this point, someone might object that the authors got some fairly low p-values. They even used Bonferroni correction, which shows that they’re trying to do things right. But I’m still unmoved, and there are two reasons for that:

• I have a skeptical prior.
• The study has low power to detect a small effect.

To understand the problems with low power, I highly recommend this article recently featured on Andrew Gelman’s blog. Or just look at this picture.

Here’s my thought process:

1. I know the effect isn’t zero, but I don’t think it’s far from zero either.
2. Assuming I’m right, this study has low power. (20 people per group!)
3. Low-power studies overestimate effect sizes. Even the sign is doubtful.
4. Therefore, this study offers only weak evidence for its claimed effect, damn the p-value.

Lessons

I’m reminded of that other study that used EEGs, and how everybody took turns pointing out how shitty it was. That was nice. Why didn’t that happen this time? I think it’s for a few reasons:

1. It got promoted by the NYT.
2. Everyone hates the NYT, so the study looked bad by association.
3. That study was also bad in ways that were unique to it.

I think the first two reasons are the most salient. The dirty secret of the rationalist community is that none of them actually knows anything about statistics. They all claim to be Bayesian, but all that means is they know Bayes’ theorem. Big whoop. I’d like to see more rationalists seriously try learning statistics. Download R, get a copy of Statistical Rethinking, and start following Andrew Gelman. (He can be annoying sometimes. Follow him anyway.) And for the love of god, be more skeptical of small, sensational studies!